Essentially all models are wrong, but some are useful (George Box).

Pada dasarnya, semua model itu salah, tapi sebagian model itu berguna.

Pernyataan yang menggelitik ini disampaikan oleh George Box, seorang pakar statistika yang pernah dipercaya menjadi Presiden dari American Statistical Association. Dalam masa pandemi Covid-19 ini, para ahli dari berbagai disiplin ilmu baik di dalam negeri maupun di luar negeri giat mempublikasikan model-model yang memprediksi naik turunnya jumlah kasus Covid-19. Di antara model-model terbaru yang muncul adalah sebuah model yang dipublikasikan oleh Fábio A.M.Cássaro dan Luiz F.Pires, dua orang peneliti dari State University of Ponta Grossa, Brasil. Model yang mereka tulis terbit sekitar sebulan yang lalu, tepatnya tanggal 20 April 2020 di Science of the Total Environment, sebuah jurnal internasional bereputasi yang terindeks Scopus dengan peringkat Q1 di bidang teknik lingkungan. Artikel mereka ini bersifat open access sehingga dapat kita unduh secara gratis (lihat URL-nya pada Referensi).

Model Matematika

Para peneliti ini menggunakan sebuah persamaan matematika sederhana yang mula-mula dipublikasikan oleh P.A. Zandbergen dan J. Chakraborty pada International Journal of Health Geographics pada tahun 2006.

Model matematika ini mereka tampilkan dalam dua fungsi yang menjadi model bagi dua hal. Hal pertama yang dimodelkan adalah jumlah kasus positif Covid-19 secara akumulasi. Hal kedua yang dimodelkan adalah jumlah kasus positif yang baru terdeteksi saja.

Jumlah kasus positif Covid-19 secara akumulasi.ditampilkan sebagai sebuah fungsi distribusi kumulatif sebagai berikut.

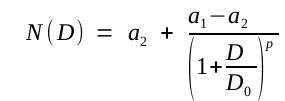
Adapun jumlah kasus positif yang baru terdeteksi saja dimodelkan sebagai turunan pertama fungsi di atas terhadap jumlah hari.

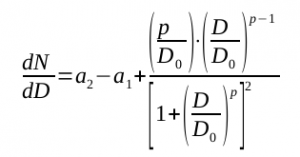
Dalam kedua persamaan ini, D adalah jumlah hari yang sudah terlewati setelah kasus pertama Covid-19 terdeteksi. N(D) berarti jumlah kasus positif Covid-19 sebagai fungsi D. Sementara itu, a1, a2, dan p merupakan adjustment parameters, yaitu parameter-parameter tertentu yang nilainya dapat menyesuaikan diri dengan data. Nantinya setelah analisis data dilakukan, didapati bahwa a1 ini terkait dengan ekstrapolasi kurva jumlah kasus Covid-19 untuk nilai D yang kecil, yang berarti bahwa a1 ini ekstrapolasi kurva untuk pandemi di masa awal kemunculannya. Sementara itu, a2 merupakan ekstrapolasi kurva untuk D yang besar, yaitu ketika pandemi sudah di masa stabil. Do didapati sebagai nilai yang dekat dengan titik perubahan kurva, dekat dengan titik maksimum untuk jumlah kasus-kasus baru. Adapun p didapati sebagai tingkat laju pertumbuhan jumlah kasus. Nilai p yang besar terkait dengan kurva pandemi yang tiba-tiba naik tajam pada masa awal. Sebaliknya, nilai p yang kecil terkait dengan pertumbuhan kurva pandemi yang landai pada masa awal.

Data

Data yang digunakan oleh para peneliti adalah data-data jumlah kasus positif Covid-19 secara akumulasi dan data-data jumlah kasus yang baru terdeteksi di China, Italia, Spanyol, Jerman, dan Austria. Para peneliti ini merujuk pada data pada Worldometers. 

Hasil

Model matematika yang digunakan ini berhasil menjelaskan jumlah kasus positif Covid-19 secara akumulasi di China dengan sangat baik, ditandai dengan r2 = 0,9912. Pada kasus di Italia, model sebelumnya menggunakan basis fungsi eksponensial. Ternyata model eksponensial tersebut gagal memprediksi jumlah kenaikan kasus yang terjadi tiba-tiba sehingga untuk hari ke-21 saja kesalahan prediksinya sudah mencapai  100%.

Ternyata, selain sesuai untuk China, model yang diusulkan para peneliti di artikel ini berhasil meyesuaikan diri dengan data pada masa pandemi Italia, Spanyol, Jerman, dan Austria dengan bukti visual yang jelas.

Referensi

Cássaro, F. A. M., & Pires, L. F. (2020). Can we predict the occurrence of COVID-19 cases? Considerations using a simple model of growth. Science of the Total Environment, 728, 138834. https://doi.org/10.1016/j.scitotenv.2020.138834

 

 

 

 

Posted on: May 31, 2020, by : Abdur Rohman